Bilinear Spatiotemporal Basis Models
3 The Robotics Institute
Carnegie Mellon University
2 Disney Research
Pittsburgh
1 LUMS
School of Science & Engineering
Abstract
A variety of dynamic objects, such as faces, bodies, and cloth, are represented in computer graphics as a collection of moving spatial landmarks. Spatiotemporal data is inherent in a number of graphics applications including animation, simulation, and object and camera tracking. The principal modes of variation in the spatial geometry of objects are typically modeled using dimensionality reduction techniques, while concurrently, trajectory representations like splines and autoregressive models are widely used to exploit the temporal regularity of deformation. In this article, we present the bilinear spatiotemporal basis as a model that simultaneously exploits spatial and temporal regularity while maintaining the ability to generalize well to new sequences. This factorization allows the use of analytical, predefined functions to represent temporal variation (e.g., B-Splines or the Discrete Cosine Transform) resulting in efficient model representation and estimation. The model can be interpreted as representing the data as a linear combination of spatiotemporal sequences consisting of shape modes oscillating over time at key frequencies. We apply the bilinear model to natural spatiotemporal phenomena, including face, body, and cloth motion data, and compare it in terms of compaction, generalization ability, predictive precision, and efficiency to existing models. We demonstrate the application of the model to a number of graphics tasks including labeling, gap-filling, de-noising, and motion touch-up.
Publication


At a glance
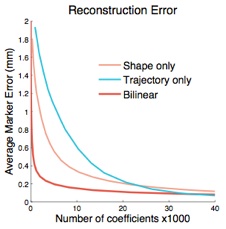
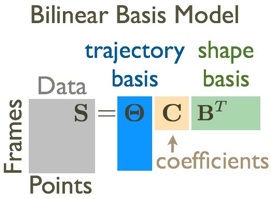
The bilinear basis model decomposes a spatiotemporal volume of data into spatial and temporal modes of variation (left). The outer product of these modes constitutes a basis of spatiotemporal modes of variation (center). This model results in higher compaction—meaning fewer coefficients—for the same error (right).
Acknowledgements
We are grateful to the following people for resources, discussions, and suggestions: Goran Milic, Rafael Tena, Moshe Mahler, Hyun Soo Park, Elizabeth Carter, Simon Lucey, and Jessica Hodgins.
Copyright notice
The documents contained in these directories are included by the contributing authors as a means to ensure timely dissemination of scholarly and technical work on a non-commercial basis. Copyright and all rights therein are maintained by the authors or by other copyright holders, notwithstanding that they have offered their works here electronically. It is understood that all persons copying this information will adhere to the terms and constraints invoked by each author's copyright. These works may not be reposted without the explicit permission of the copyright holder.
Video
Example Code
This example MATLAB code is provided as a companion to the paper and illustrates the main algorithms related to the bilinear model. The code was written for clarity rather than for speed or stability. [ bilinear_toolbox_v01.zip (ZIP, 8 MB) ]