 |

|
 |

|
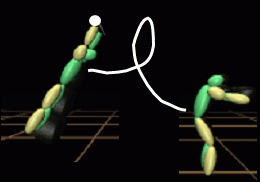
Our goal is to provide a way to create pleasing animations from a very small amount of input data. For example, the figure at the top of the page shows a sketch that suggests an initial pose with contact on the high bar, a final pose with contact at the ground, and a dismount that includes a backflip. From information such as this, we would like to create a physically plausible dismount such as that shown in the filmstrip just below the sketch.
One common way to tackle this problem is through optimization. The user's input provides a very rough initial guess, and the motion is improved using an iterative process.
Making optimization work for complex, humanlike characters, however, has been a challenge. The history of previous work suggests that six or so degrees of freedom can be handled without difficulty. Expanding beyond this limit requires some additional information --- typically a very good initial guess, reduction in the effective degrees of freedom of the character, or turning off constraints such as those that enforce correct physics. The primary insight of this work is to suggest a different way to make this problem tractable while including many common constraints that enforce physical correctness. In particular, we show that constraints on aggregate forces (forces applied by the character to its environment) can be handled efficiently.
To start, we note that some variations of this optimization problem are inherently more complex than others. One major difference is in the time required to collect all of the first derivatives that are used as part of any gradient-based optimization process. For some ("difficult") problem formulations, this time is quadratic in the degrees of freedom of the character. For example, minimizing the sum of squared joint torques has this property. For other ("easier") problem formulations, all derivatives can be obtained in time linear in the character's degrees of freedom.
If we can consider problem formulations with linear time first derivatives to be "easy," then a good question to ask is what problem formulations have this linear time property? Two such families are problems with constraints and objectives on kinematic parameters and problems with constraints and objectives on the aggregate force applied by the character to its environment.
The simplest formulations where all first derivatives can be collected in linear time use kinematic constraints and objective functions. These include functions of the positions, velocities and accelerations of points on the character as well as joint angle positions and their derivatives. Kinematic constraints have long been noted to lead to tractable problems. Typical members of this family are:
The limitation of kinematic constraints is that they include relatively few of the common types of constraints used to enforce correct physics. We have found that a second group of constraints also leads to linear time first derivatives. These are functions of aggregate forces, which are forces between the character and the environment. This family does include many common physics constraints. For example:

|
Computing all first derivatives in linear time for aggregate force constraints is trickier than for kinematic constraints and requires rewriting equations of motion for this purpose. We show how this can be done in our SIGGRAPH 2003 paper (listed below).
Here are stills of some results obtained using our approach. An overview movie can be found below.

|