 Programming Project #2 for the 15-862 class (proj2g)
Programming Project #2 for the 15-862 class (proj2g)15-463: Computational Photography
 Programming Project #2 for the 15-862 class (proj2g)
Programming Project #2 for the 15-862 class (proj2g)
This project explores Eulerian Video Magnification to reveal temporal image variations that tend to be difficult to visualize. This video briefly describes the technique, and shows a variety of visual effects attainable with it. For example, one can amplify blood flow and low-amplitude motion with Eulerian Magnification without needing to perform image segmentation or computing optical flow.
The primary goal of this assignment is to amplify temporal color variations in two videos (face and baby2), and amplify color or slow-amplitude motion in your own custom short video sequence that you record yourself. For this you will read the paper about Eulerian Video Magnification and implement the approach.
How can you amplify image variations that are hard to see with the naked eye? The insight is that some of these hard-to-see changes occur at particular temporal frequencies that we can augment using simple filters in the frequency domain! For example, to magnify pulse we can look at pixel variations with frequencies between 0.4 and 4Hz, which correspond to 24 to 240 beats per minute.
The Eulerian magnification process is straight forward:
(1) An image sequence is decomposed into different spatial frequency bands
using Laplacian pyramids
(2) The time series corresponding to the value of a pixel on all levels of the pyramid are band-pass
filtered to extract frequency bands of interest
(3) The extracted band-passed signals are multiplied by a magnification factor and this result is added to the original signals
(4) The magnified signals that compose the spatial pyramid are collapsed to obtain the final output
If the input video has multiple channels (e.g., each frame is a color image in RGB color space), then we can process each channel independently. The YIQ color space is particularly suggested for Eulerian magnification since it allows to easily amplify intensity and chromaticity independently of each other (we can use rgb2ntsc and ntsc2rgb to move between RGB and YIQ in MATLAB).
The hard part of the process is to find the right parameters to get the desired magnification effect. For example, one can change the size of the Laplacian pyramid, multiply the time series corresponding to the value of a pixel by different scale factors at different levels of the pyramid, or attenuate the magnification when adding the augmented band-passed signals to the original ones. The choice of the band-pass filter (e.g., the range of frequencies it passes/rejects, its order, etc.) can also influence the obtained results. This exploration is part of the project, so you should start early!
The first step to augment a video is to compute a Laplacian pyramid for every single frame (see Szeliski's book, section 3.5.3). The Laplacian pyramid was originally proposed by Burt and Adelson in their 1983 paper The Laplacian pyramid as a compact image code, where they suggested to sample the image with Laplacian operators of many scales. This pyramid is constructed by taking the difference between adjacent levels of a Gaussian pyramid, and approximates the second derivative of the image, highlighting regions of rapid intensity change.
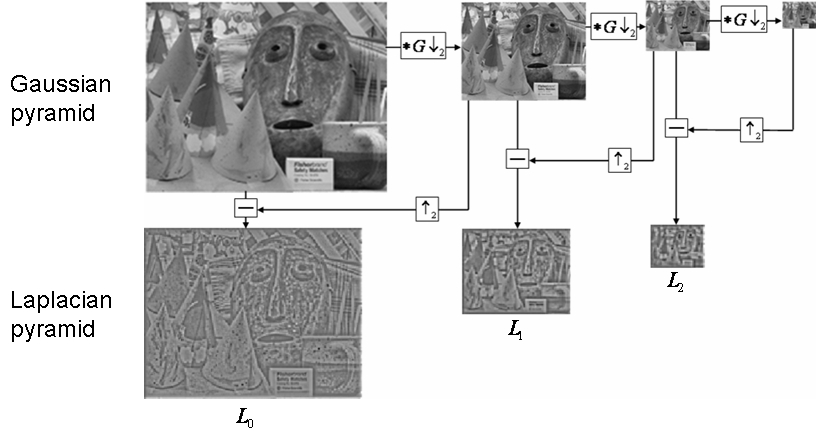
Each level of the Laplacian pyramid will have different spatial frequency information, as shown in the picture above. Notice that we need to upsample one of the images when computing the difference between adjacent levels of a Gaussian pyramid, since one will have a size of wxh, while the other will have (w/2)x(h/2) pixels. Since the last image in the Gaussian pyramid does not contain an adjacent image to perform the subtraction, then it just becomes the last level of the Laplacian pyramid.
Notice that by doing the inverse process of constructing a Laplacian pyramid we can reconstruct the original image. In other words, by upsampling and adding levels of the Laplacian pyramid we can generate the full-size picture. This reconstruction is necessary to augment videos using the Eulerian approach.
We consider the time series corresponding to the value of a pixel on
all spatial levels of the Laplacian pyramid. We convert this time
series to the frequency domain using the Fast Fourier Transform
(fft in MATLAB), and apply a band pass filter to this
signal. The choice of the band-pass filter is crucial, and we recommend
designing and visualizing the filter with fdatool
and fvtool in MATLAB
(see an example by MathWorks).
To make this process easier, we provide you with a butterworthBandpassFilter function to
generate a Butterworth band-pass filter of a particular order. This
function was generated with fdatool, and is optional for you to use. You can download the
file, or use the code below for reference:
% Hd = butterworthBandpassFilter(Fs, N, Fc1, Fc2)
% Fs - sampling frequency (e.g., 30Hz)
% N - filter order (must be an even number)
% Fc1 - first cut frequency
% Fc2 - second cut frequency
% Hd - approximate ideal bandpass filter
function Hd = butterworthBandpassFilter(Fs, N, Fc1, Fc2)
h = fdesign.bandpass('N,F3dB1,F3dB2', N, Fc1, Fc2, Fs);
Hd = design(h, 'butter');
end
More details on the fdesign.bandpass parameters can be
found here. Check
the Eulerian Video
Magnification paper
for details on the parameters they used on the face and
baby2 videos. You will have to find the right parameters for the other video that you capture yourself, and process.
In order to filter the time series of the pixels fast, we
recommend you perform this operation in the frequency domain, since
multiplication is faster than convolution. But be careful
about fft's output format when doing this! As explained
in this
tutorial, the DC component of fftx = fft(x),
for x a 1D signal, is the first
element fftx(1) of the array. If x has an
even number of samples, then the magnitude of the FFT will be
symmetric, such that the first (1+nfft/2) points are unique, and the
rest are symmetrically redundant. The
element fftx(1+nfft/2) is the Nyquist frequency component
of x in this case. If the number of samples
of x is odd, however, the Nyquist frequency component is
not evaluated, and the number of unique points is (nfft+1)/2.
Also, if you decide to use the butterworthBandpassFilter
function, then you will need to get the frequency components of the filter
for fast computation. This can be done by using
MATLAB's freqz
function, by passing the filter and the length of the output that you
want (i.e., fftHd = freqz(Hd,NumSamples)). Again, be careful about
how the frequency components are output by freqz.
After extracting the frequency band of interest, we need to amplify it and add the result back to the original signal.
After amplifying the signals, all that is left is to collapse the
Laplacian pyramids into a single image per frame. Notice that we can attenuate the amplification to obtain different resuts, or we can low-pass filter the amplified signal to reduce effects on high frequency components of the images, such as borders. Two different
blood flow amplification effects on the face.mp4 image sequence
are presented below,
Try some special moves to increase your score:
Use both words and images to show us what you've done (describe in detail your algorithm parameterization for each of your results).
Place all code in your code/ directory. Include a README describing the contents of each file.
In the website in your www/ directory, please: