A Point-based Method for Animating Incompressible Flow
| FunShing Sin | Adam W. Bargteil | Jessica K. Hodgins |
Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation (2009)
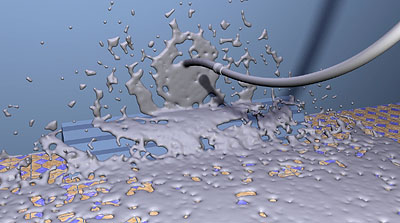
In this paper, we present a point-based method for animating incompressible flow. The advection term is handled by moving the sample points through the flow in a Lagrangian fashion. However, unlike most previous approaches, the pressure term is handled by performing a projection onto a divergence-free field. To perform the pressure projection, we compute a Voronoi diagram with the sample points as input. Borrowing from Finite Volume Methods, we then invoke the divergence theorem and ensure that each Voronoi cell is divergence free. To handle complex boundary conditions, Voronoi cells are clipped against obstacle boundaries and free surfaces. The method is stable, flexible and combines many of the desirable features of point-based and grid-based methods. We demonstrate our approach on several examples of splashing and streaming liquid and swirling smoke.
FunShing Sin, Adam W. Bargteil, Jessica K. Hodgins (2009). A Point-based Method for Animating Incompressible Flow. Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation.
@inproceedings{Sin:2009:APB,
author = "FunShing Sin and Adam W. Bargteil and Jessica K. Hodgins",
title = {A Point-based Method for Animating Incompressible Flow},
booktitle = {Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation},
year = {2009},
month = {Aug},
location = {New Orleans,Louisiana},
}

