Differential walk on spheres
| Bailey Miller | Rohan Sawhney | Keenan Crane | Ioannis Gkioulekas |
ACM Trans. Graph. (2024)
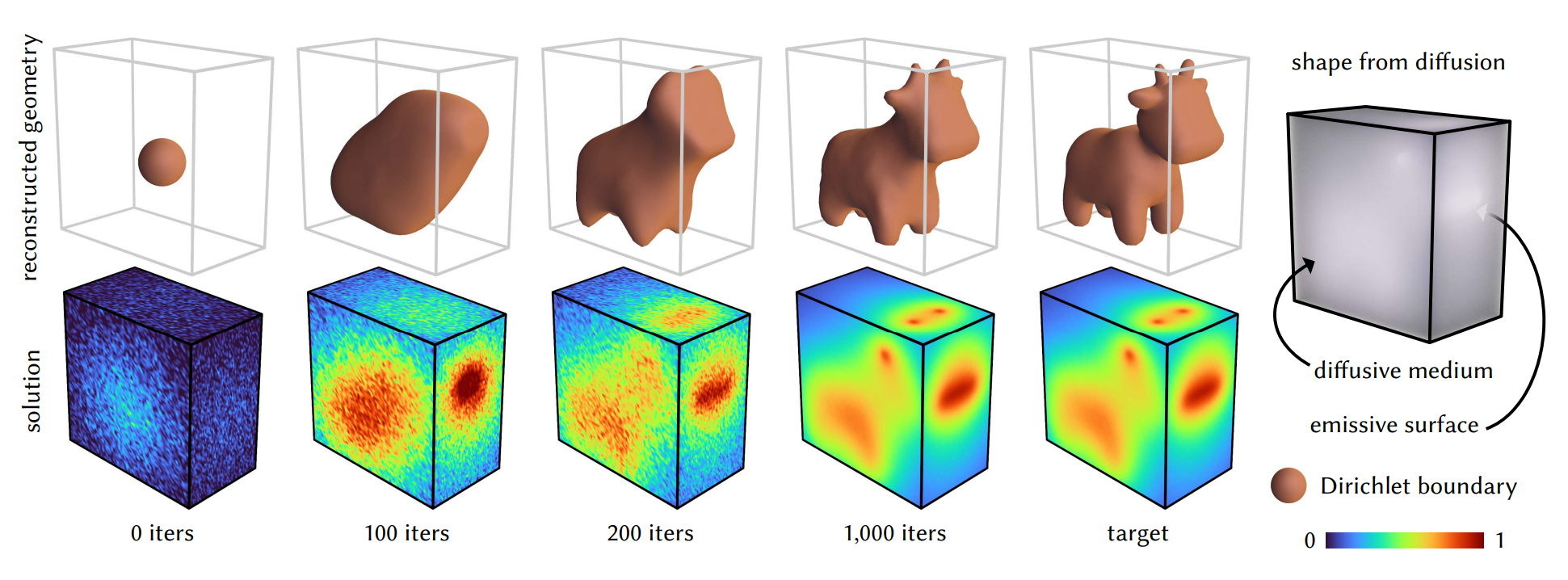
We introduce a Monte Carlo method for computing derivatives of the solution to a partial differential equation (PDE) with respect to problem parameters (such as domain geometry or boundary conditions). Derivatives can be evaluated at arbitrary points, without performing a global solve or constructing a volumetric grid or mesh. The method is hence well suited to inverse problems with complex geometry, such as PDE-constrained shape optimization. Like other walk on spheres (WoS) algorithms, our method is trivial to parallelize, and is agnostic to boundary representation (meshes, splines, implicit surfaces, etc.), supporting large topological changes. We focus in particular on screened Poisson equations, which model diverse problems from scientific and geometric computing. As in differentiable rendering, we jointly estimate derivatives with respect to all parameters---hence, cost does not grow significantly with parameter count. In practice, even noisy derivative estimates exhibit fast, stable convergence for stochastic gradient-based optimization, as we show through examples from thermal design, shape from diffusion, and computer graphics.
Bailey Miller, Rohan Sawhney, Keenan Crane, Ioannis Gkioulekas (2024). Differential walk on spheres. ACM Trans. Graph..
@article{Miller:2024:DiffWoS,
author = {Bailey Miller, Rohan Sawhney, Keenan Crane, Ioannis Gkioulekas},
title = {Differential walk on spheres},
journal = {ACM Trans. Graph.},
year = {2024},
publisher = {ACM},
address = {New York, NY, USA},
}

