Boundary Value Caching for Walk on Spheres
| Bailey Miller* | Rohan Sawhney* | Keenan Crane† | Ioannis Gkioulekas† |
ACM Trans. Graph. (2023)
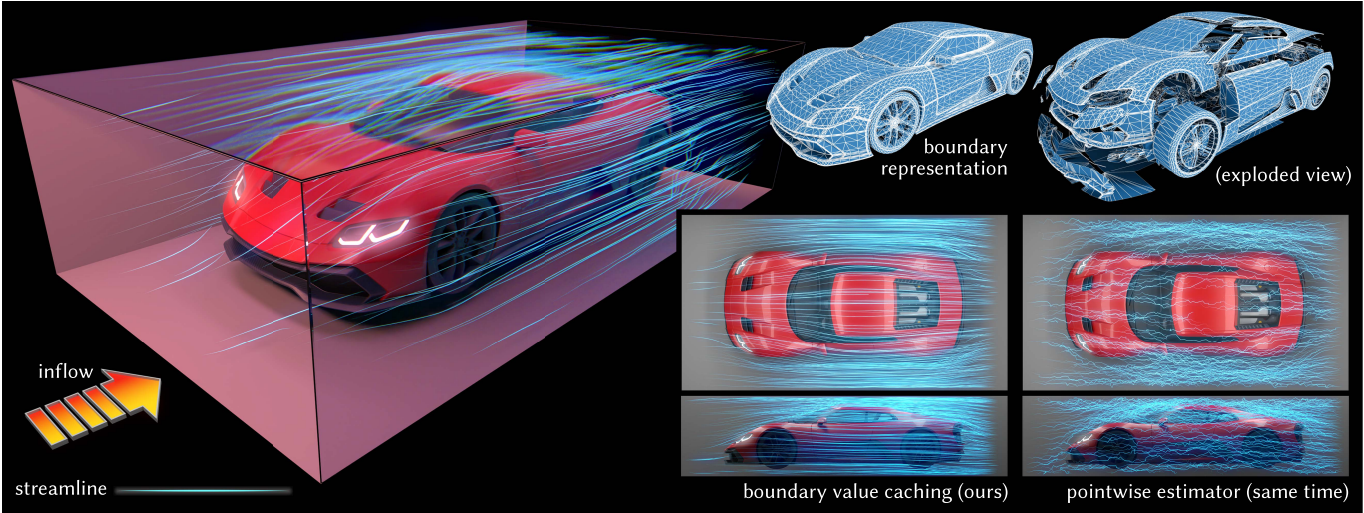
Grid-free Monte Carlo methods such as walk on spheres can be used to solve elliptic partial differential equations without mesh generation or global solves. However, such methods independently estimate the solution at every point, and hence do not take advantage of the high spatial regularity of solutions to elliptic problems. We propose a fast caching strategy which first estimates solution values and derivatives at randomly sampled points along the boundary of the domain (or a local region of interest). These cached values then provide cheap, output-sensitive evaluation of the solution (or its gradient) at interior points, via a boundary integral formulation. Unlike classic boundary integral methods, our caching scheme introduces zero statistical bias and does not require a dense global solve. Moreover we can handle imperfect geometry (e.g., with self-intersections) and detailed boundary/source terms without repairing or resampling the boundary representation. Overall, our scheme is similar in spirit to virtual point light methods from photorealistic rendering: it suppresses the typical salt-and-pepper noise characteristic of independent Monte Carlo estimates, while still retaining the many advantages of Monte Carlo solvers: progressive evaluation, trivial parallelization, geometric robustness, etc. We validate our approach using test problems from visual and geometric computing.
Bailey Miller*, Rohan Sawhney*, Keenan Crane†, Ioannis Gkioulekas† (2023). Boundary Value Caching for Walk on Spheres. ACM Trans. Graph..
@article{Miller:2023:BVC,
author = {Bailey Miller* and Rohan Sawhney* and Keenan Crane† and Ioannis Gkioulekas†},
title = {Boundary Value Caching for Walk on Spheres},
journal = {ACM Trans. Graph.},
year = {2023},
publisher = {ACM},
address = {New York, NY, USA},
}

