A Dirac Operator for Extrinsic Shape Analysis
| Derek Liu | Alec Jacobson | Keenan Crane |
Computer Graphics Forum (SGP) (2017)
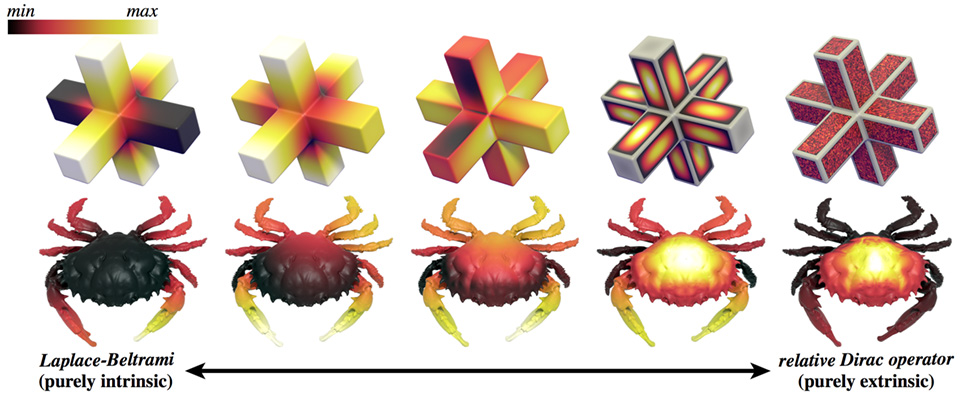
A conformal flattening maps a curved surface to the plane without distorting angles---such maps have become a fundamental building block for problems in geometry processing, numerical simulation, and computational design. Yet existing methods provide little direct control over the shape of the flattened domain, or else demand expensive nonlinear optimization. Boundary first flattening (BFF) is a linear method for conformal parameterization which is faster than traditional linear methods, yet provides control and quality comparable to sophisticated nonlinear schemes. The key insight is that the boundary data for many conformal mapping problems can be efficiently constructed via the Cherrier formula together with a pair of Poincaré-Steklov operators; once the boundary is known, the map can be easily extended over the rest of the domain. Since computation demands only a single factorization of the real Laplace matrix, the amortized cost is about 50x less than any previously published technique for boundary-controlled conformal flattening. As a result, BFF opens the door to real-time editing or fast optimization of high-resolution maps, with direct control over boundary length or angle. We show how this method can be used to construct maps with sharp corners, cone singularities, minimal area distortion, and uniformization over the unit disk; we also demonstrate for the first time how a surface can be conformally flattened directly onto any given target shape.
Derek Liu, Alec Jacobson, Keenan Crane (2017). A Dirac Operator for Extrinsic Shape Analysis. Computer Graphics Forum (SGP), 36(5).
@article{Liu:2017:DOE,
author={Derek Liu and Alec Jacobson and Keenan Crane},
title={A Dirac Operator for Extrinsic Shape Analysis},
journal={Computer Graphics Forum (SGP)},
volume={36},
number={5},
year={2017},
}

